

ℹ️ 목차
그래프 이론
│
├── 1. 그래프에 대해서
│ ├── 1.1 그래프의 정의
│ └── 1.2 핵심 용어
│
├── 2. 그래프의 표현 방법
│ ├── 2.1 인접 행렬 (Adjacency Matrix)
│ └── 2.2 인접 리스트 (Adjacency List)
│
├── 3. 그래프의 종류
│ ├── 3.1 방향 그래프 (Directed Graph)
│ ├── 3.2 무방향 그래프 (Undirected Graph)
│ ├── 3.3 가중치 그래프 (Weighted Graph)
│ ├── 3.4 연결 그래프 (Connected Graph)
│ ├── 3.5 비순환 그래프 (Acyclic Graph)
│ │ └── DAG (Directed Acyclic Graph)
│ ├── 3.6 이분 그래프 (Bipartite Graph)
│ ├── 3.7 완전 그래프 (Complete Graph)
│ ├── 3.8 트리 (Tree)
│ │ ├── 일반 트리
│ │ ├── 이진 트리 (Binary Tree)
│ │ ├── 이진 탐색 트리 (BST)
│ │ ├── AVL 트리
│ │ ├── 레드-블랙 트리
│ │ ├── B-트리
│ │ └── 힙 (Heap)
│ └── 3.9 평면 그래프 (Planar Graph)
│
└── 4. 연관 알고리즘
├── 4.1 그래프 탐색
│ ├── DFS (Depth-First Search)
│ └── BFS (Breadth-First Search)
│
├── 4.2 최단 경로
│ ├── Dijkstra
│ ├── Bellman-Ford
│ └── Floyd-Warshall
│
├── 4.3 최소 신장 트리 (MST)
│ ├── Kruskal
│ └── Prim
│
├── 4.4 위상 정렬 (Topological Sort)
│ ├── 진입 차수 방법 (Kahn's Algorithm)
│ └── DFS 방법
│
├── 4.5 트리 알고리즘
│ ├── 트리 순회 (Tree Traversal)
│ └── 최소 공통 조상 (LCA)
│
└── 4.6 유니온 파인드 (Union-Find)
├── 기본 구현
├── 경로 압축
└── Union by Rank🅿️ 포스트 목록
| 그래프 이론 (Graph Theory) - 1. 그래프에 대해서 |
| 그래프 이론 (Graph Theory) - 2. 그래프의 표현 방법 |
1️⃣ 그래프의 표현 방법
그래프를 컴퓨터에서 표현하는 방법은 크게 인접 행렬(Adjacency Matrix)과 인접 리스트(Adjacency List) 두 가지가 있다.
각각의 방법은 서로 다른 트레이드오프를 가지고 있어서, 그래프의 특성과 수행할 연산에 따라 적절한 방법을 선택해야 한다.
✅ 인접 행렬 (Adjacency Matrix)

🔹개념
정점(vertex)의 개수가 n개일 때, n×n 크기의 2차원 배열을 사용하여 그래프를 표현한다.
배열의 [i][j] 위치의 값은 정점 i에서 정점 j로 가는 간선의 존재 여부(또는 가중치)를 나타낸다.
🔹이렇게 구현하는 이유
행렬이라는 수학적 구조를 사용하면 그래프를 매우 직관적으로 표현할 수 있다.
행렬은 본래 두 집합 간의 관계를 나타내는 도구로 행은 "출발 정점", 열은 "도착 정점"으로 자연스럽게 이해할 수 있다.
또한 행렬은 배열로 구현할 수 있고 배열의 인덱싱은 O(1)이므로, 두 정점 사이의 연결 관계를 즉시 확인할 수 있다는 점이 핵심 아이디어.
🔹장점
- 간선 존재 여부 확인이 매우 빠름: 두 정점 i와 j 사이에 간선이 있는지 O(1)에 확인 가능
- 구현이 단순함: 2차원 배열만 있으면 되므로 코드가 간결
- 밀집 그래프(dense graph)에 효율적: 간선이 많을 때 공간 낭비가 적음
- 그래프 연산이 용이함: 행렬 곱셈 등 수학적 연산을 통해 경로 찾기 등이 가능
🔹단점
- 공간 복잡도가 높음: 항상 O(n²)의 공간이 필요. 간선이 적어도 전체 행렬을 유지해야 함
- 희소 그래프(sparse graph)에 비효율적: 간선이 적을 때 대부분의 공간이 낭비됨
- 또한 정점이 너무 많을 때도 메모리 측면에서 오버헤드가 커지기 때문에 고려해야 할 부분 중 하나.
- 모든 인접 정점 탐색이 느림: 특정 정점의 모든 이웃을 찾으려면 O(n)이 필요 ※연결 여부 확인 과정 때문
🔹사용 시기
- 간선의 개수가 정점 개수의 제곱에 가까울 때 (밀집 그래프)
- 두 정점 사이의 연결 여부를 자주 확인해야 할 때
- 정점의 개수가 많지 않을 때 (메모리 제약이 없을 때)
- 256MB 제한 기준 : 정점 N은 약 8,000이 경계선
- 그래프 이론의 수학적 연산을 수행할 때
🔹구현 방법 (JAVA)
✅ 인접 리스트 (Adjacency List)
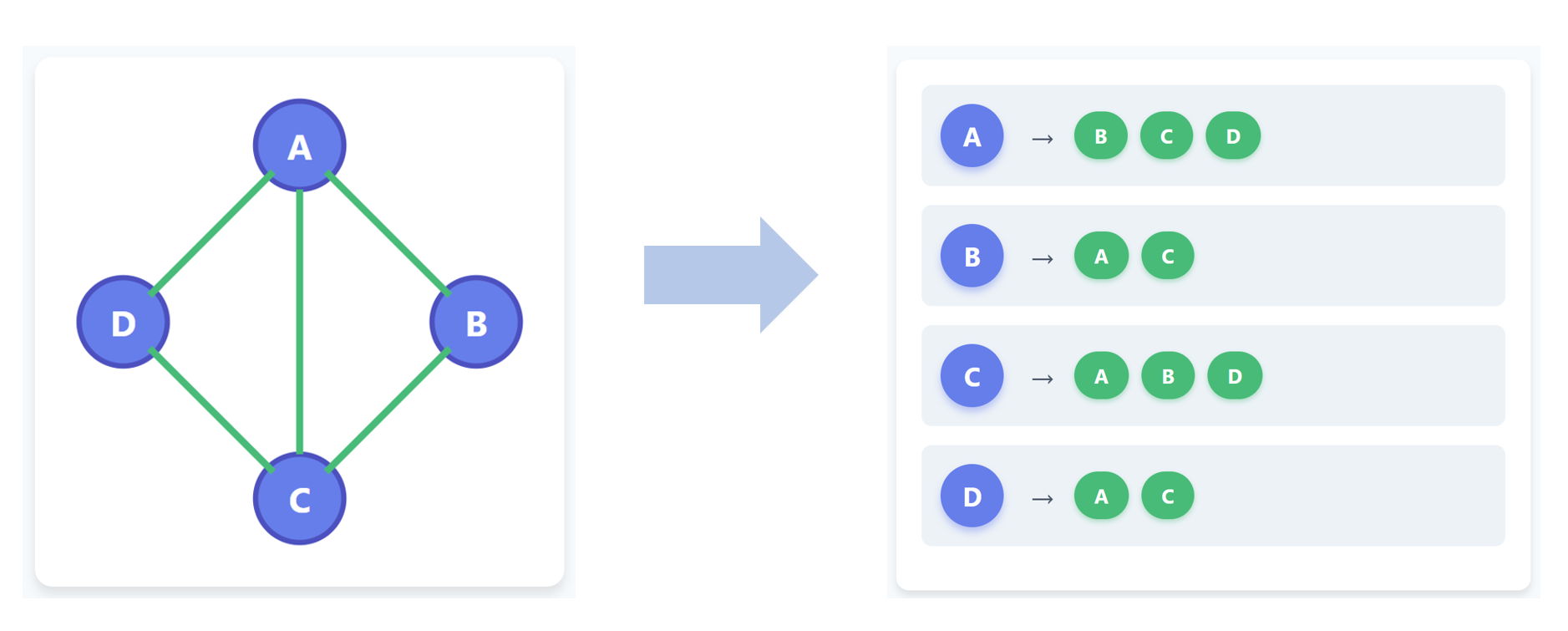
🔹개념
각 정점마다 그 정점과 연결된 정점들의 리스트를 유지하는 방식이다.
각 정점을 배열 또는 리스트를 통해 인덱스로 구성하고, 그 값으로 연결된 정점들의 리스트(또는 연결 리스트)를 저장.
주요 차이점은 연결이 되지 않은 두 집합을 위한 메모리 할당이 없다는 것이다.
🔹이렇게 구현하는 이유
실제 존재하는 간선 정보만 저장하자는 것이 핵심 아이디어.
대부분의 실제 그래프는 희소 그래프이므로, 존재하지 않는 간선까지 저장할 필요가 없다.
🔹장점
- 공간 효율적: O(n + e) ※n은 정점 수, e는 간선 수
- 희소 그래프에 최적: 실제 간선만 저장하므로 낭비가 없음
- 인접 정점 순회가 빠름: 특정 정점의 모든 이웃을 O(degree) 시간에 탐색 가능
- 동적 그래프에 유리: 정점 추가/삭제가 인접 행렬에 비해 상대적으로 용이
🔹단점
- 간선 존재 여부 확인이 느림: 두 정점이 연결되었는지(혹은 안되었는지) 확인하려면 최악의 경우 O(n) 필요
- 구현이 상대적으로 복잡함: 리스트나 동적 자료구조를 관리해야 함
- 캐시 효율성이 떨어질 수 있음: 포인터를 따라가야 하므로 메모리 접근 패턴이 불규칙
🔹사용 시기
- 간선의 개수가 정점 개수에 비해 적을 때 (희소 그래프)
- 그래프 탐색 알고리즘(BFS, DFS)을 수행할 때
- 정점의 개수가 매우 많을 때
- 나의 경우 웬만하면 인접 리스트로 구현하는 편.
🔹구현 방법 (JAVA)
'CS > 자료구조' 카테고리의 다른 글
| 그래프 이론 (Graph Theory) - 1. 그래프에 대해서 (0) | 2025.10.26 |
|---|---|
| 세그먼트 트리 (Segment Tree) (0) | 2024.11.27 |
| 트리의 특성과 종류, 구현 (0) | 2024.11.26 |
| 이분 그래프(Bipartite Graph) (0) | 2023.11.30 |

개발 기술 블로그, Dev
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!


