![[알고리즘] Union-Find (부제 : 좌표 압축은 왜?)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fct4P6J%2FbtsK153PXxD%2FAAAAAAAAAAAAAAAAAAAAAPg8wK1DhfUkNC2nWMgaMnhflTZ41hX7BB6uGg18Zs69%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DH02h4HIKg1dQY5Qw0Dyj9i4qEig%253D)

Union-Find?
분리 집합이라고도 불리는 유니온 파인드는 그래프 형태의 자료구조에서 정점들의 연결 정보를 알고 싶을 때 사용하는 알고리즘입니다.
분리 집합이라고 불리는 이유는 서로 연결된 정점들을 각각의 집합으로 만들기 때문입니다.
DFS(BFS) VS Union Find
그래프 형태의 자료에서 연결 정보를 알고 싶을 때 DFS, BFS 탐색을 통해서도 알 수 있습니다.
그러나 서로 다른 모든 정점의 연결정보를 구하려면 시간이 오래 걸릴 수 밖에 없습니다.
10만개의 정점이 있고, 모든 정점이 서로 연결되있을수도 있다면 두 정점의 연결관계를 탐색하는데 최대 10만번의 탐색이 이루어질 수 있기 때문입니다.
또한 이러한 연결관계 탐색이 N번 필요하다면 O(N^2)의 시간이 필요합니다.
Union Find를 사용하게 되면 연결된 정점들에 대해서 루트 노드를 기록하고, 기록된 루트 노드를 통해서 다른 정점들의 연결관계를 파악하기 때문에 빠르게 정점 간의 연결 관계를 확인할 수 있습니다.
그럼 이제 Union Find의 동작과정에 대해서 상세하게 파헤쳐보겠습니다.
각 정점의 루트 노드를 기록할 parent[] 배열
각 정점이 어떤 집합에 속하는지를 기록할 parent 배열입니다.

초기에 각 정점은 자기 자신을 루트로 가지고 있습니다.
int[] parent = new int[N+1]; //정점번호가 1부터 시작
for(int i=1; i<=N; i++) parent[i] = i;정점의 루트를 찾는 find 메서드
두 정점을 하나의 집합으로 연결하기 위해서는 각 정점이 어떤 루트를 가지고 있는지 탐색해야 합니다.
이를 위해 find메서드를 활용하고, parent배열 참조를 통해서 루트 노드를 찾을 수 있습니다.
static int find(int x) {
if(parent[x] == x) return x;
return find(parent[x]);
}두 정점을 연결하는 union 메서드
두 정점을 하나의 집합으로 만들기위해 두 정점 중 하나의 정점의 루트를 다른 하나의 정점으로 변경하는 메서드입니다.
static void union(int a, int b) {
int aRoot = find(a); //a정점의 루트 탐색
int bRoot = find(b); //b정점의 루트 탐색
parent[bRoot] = aRoot; //b정점의 루트를 a정점의 루트로 변경
}언제 사용할까?
보통 그래프는 두 정점의 번호와 간선이 인접행렬 혹은 인접리스트로 입력이 들어옵니다.
이러한 두 정점 사이 간선에 대한 연결을 union 메서드의 매개변수로 넣어줌으로써 두 정점을 연결시켜줄 수 있습니다.
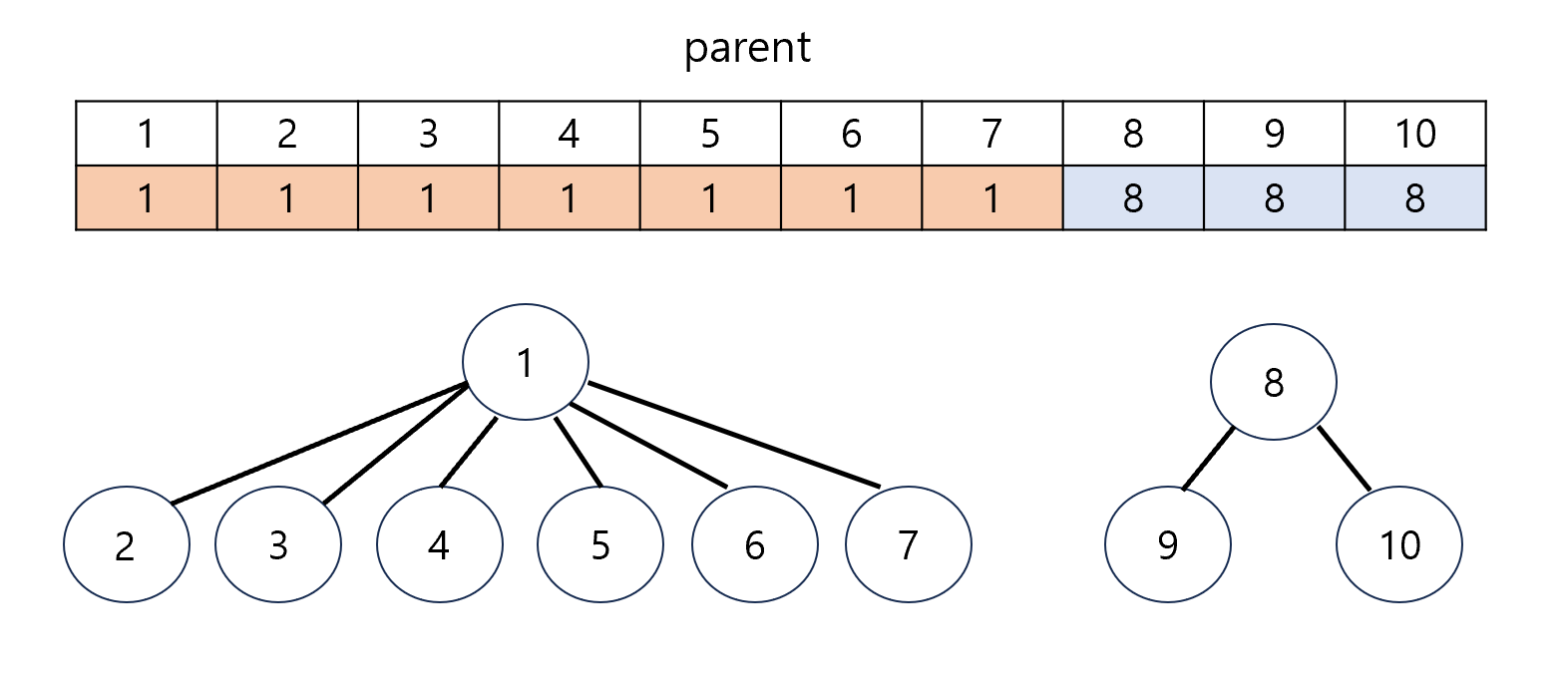
위 그림에서 union(1,7)을 수행하게 될 경우 다음처럼 변경됩니다.

1이라는 값은 두 정점의 루트값이고, 서로 다른 정점의 루트가 같다면 두 정점은 연결되어 있다고 볼 수 있습니다.
이로써 {1,7}은 1이라는 값의 같은 집합으로 합쳐진다는 것을 알 수 있습니다.
계속해서 간선에 대한 union 메서드를 수행하게 되면 다음과 같이 2개의 집합이 형성되는 걸 볼 수 있습니다.
union 메서드만으로는 제대로 된 집합을 구할 수 없다.
한 가지 예시를 들어보겠습니다.
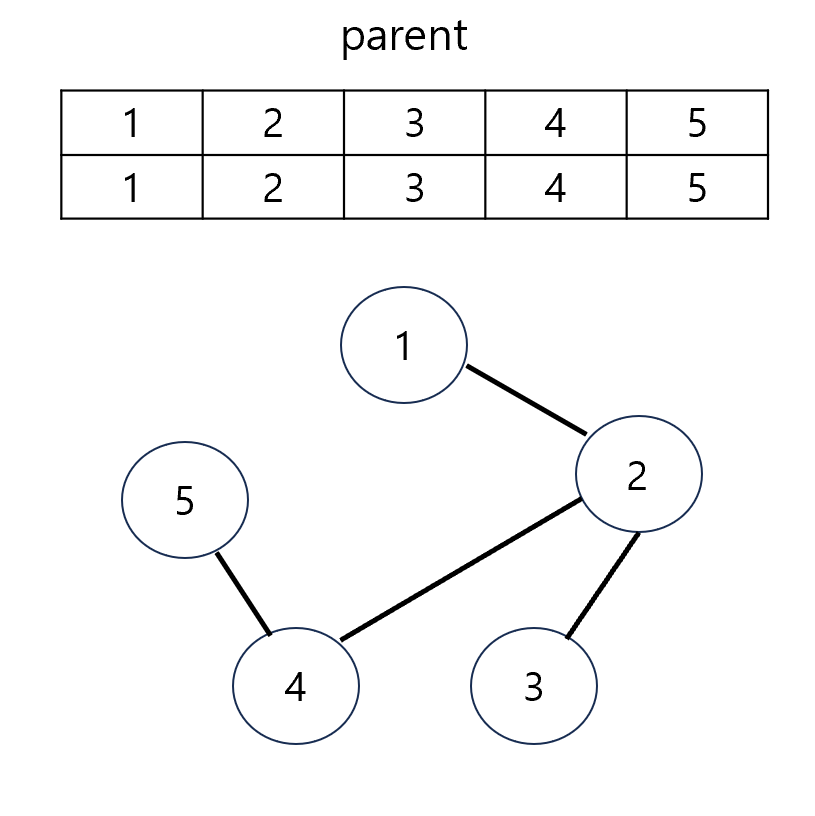
이러한 그래프가 주어졌다고 가정하고, 입력으로 들어오는 간선 정보에 대해 순차적으로 union 메서드를 수행해보겠습니다.
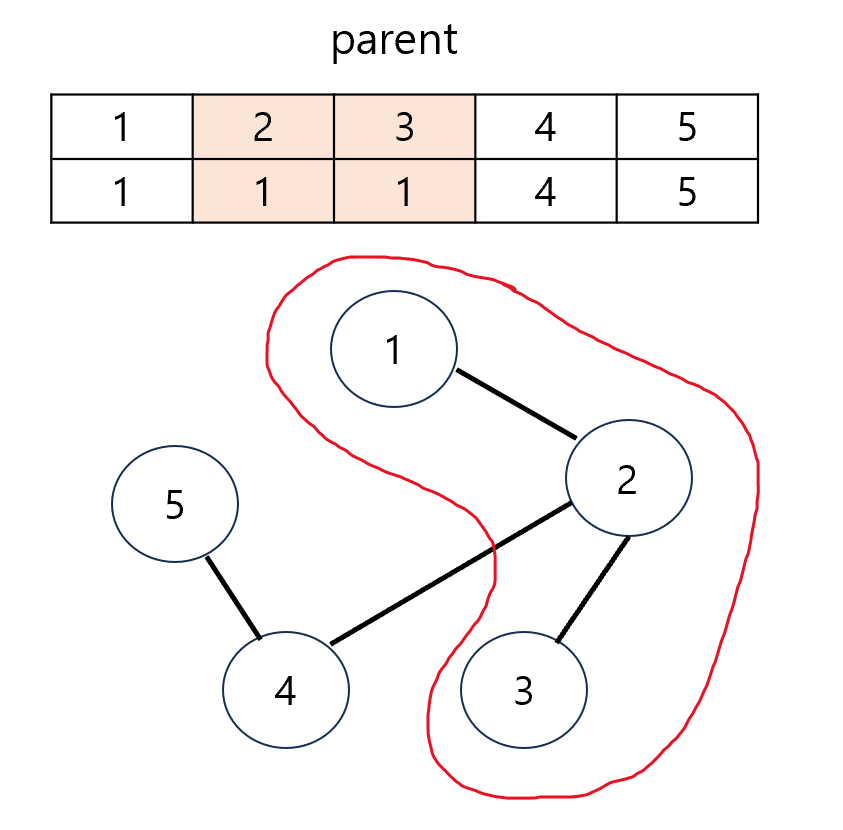
union(1,2) -> parent[2] = 1

union(2,3) -> parent[3] = 1
union(4,5) -> parent[5] = 4
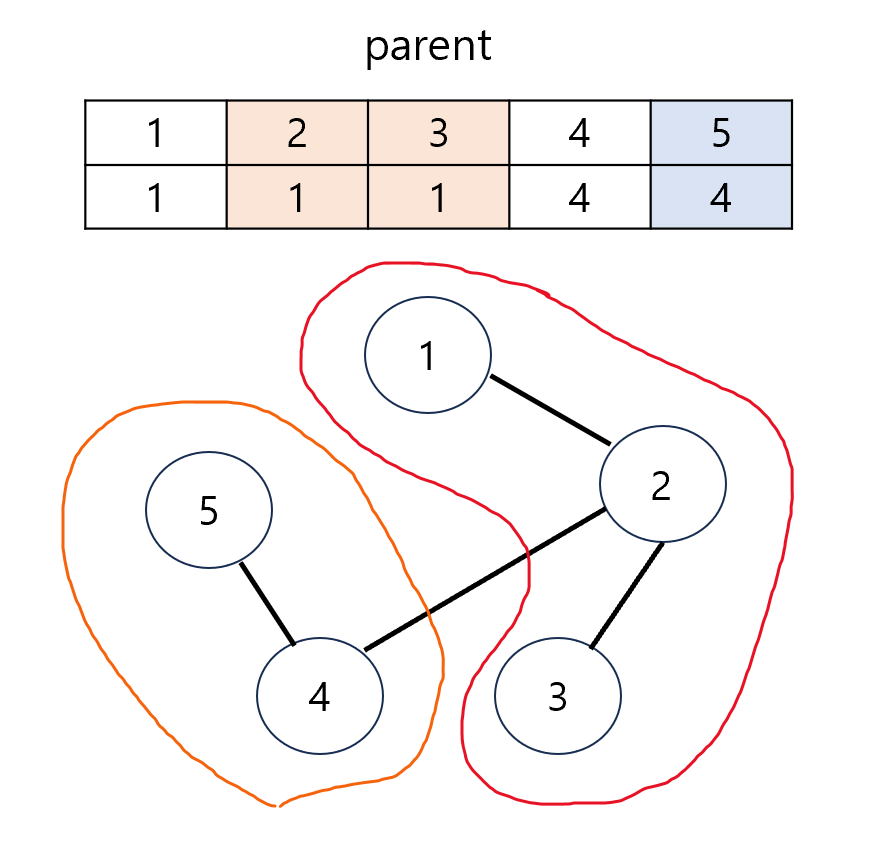
union(2,4) -> parent[4] = 1
마지막 남은 정점 2와 4의 간선 정보에 대해 union을 수행해보겠습니다.
그림 상으로는 1,2,3,4,5 모든 정점이 서로 연결되어 있고, union메서드를 통해 모든 정점이 하나의 집합으로 만들어져야 한다는 걸 머리로는 이해할 수 있습니다.
과연 결과도 똑같이 이루어질까요?
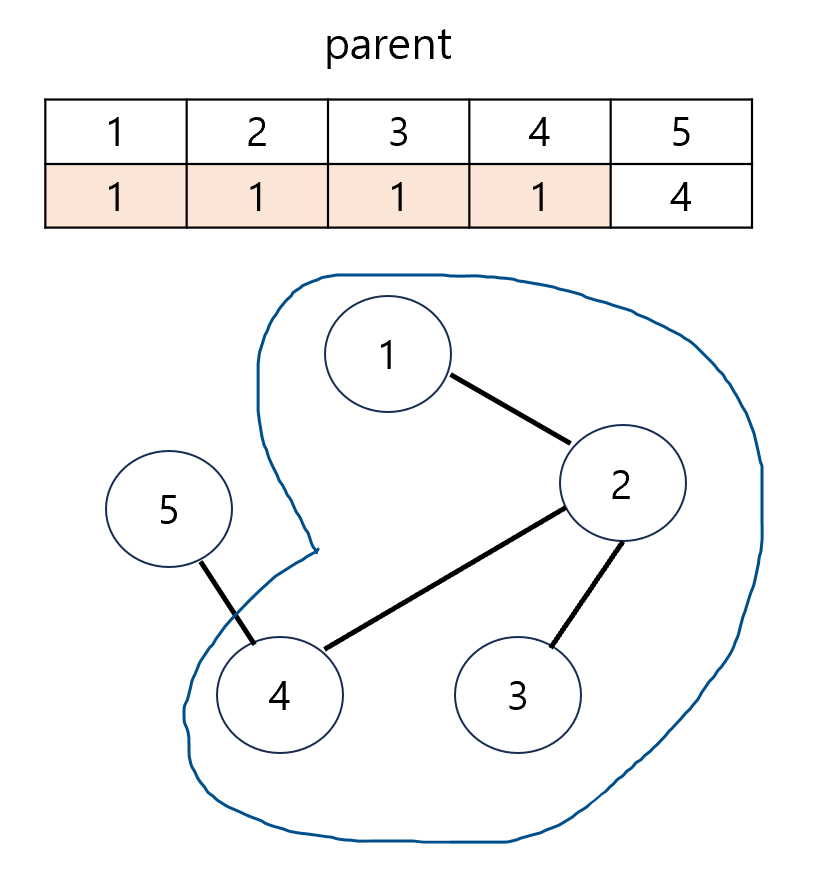
모든 간선에 대해 union을 수행하면 다음과 같은 애매한 결과가 나옵니다.
위에서 이해한대로라면 분명 4라는 집합으로 묶인 {4,5} 정점들이 모두 1이라는 집합으로 합쳐져야 할텐데 말이죠.
왜 이러한 결과가 나올까요.
union 메서드는 매개변수로 받는 두 정점의 루트 정점을 탐색하고, 두 집합을 하나의 집합으로 묶는걸 볼 수 있는데요.
메서드의 코드만 보면 알 수 있듯, 단순 입력 정점들에 대해서만 parent배열 갱신이 이루어지기 때문입니다.
그럼 제대로 된 집합을 구하지 못하는거야?
결과는 정점 5에 대한 갱신이 이루어지지 못했습니다.
그러나 find 메서드를 제대로 이해했다면, 우리는 5라는 정점에 대한 제대로 된 집합을 구할 수 있습니다.
find 메서드를 다시 설명하자면, 입력 정점에 대해 기록된 루트 정점을 마지막까지 타고 들어가서 값을 탐색합니다.
find(5)를 수행하면,
- parent[5]에는 4가 입력되있으므로 find(4)를 다시 호출합니다.
- parent[4]에는 1이 입력되있으므로 find(1)을 다시 호출합니다.
- parent[1]에는 자기 자신이 루트로 기록되있으므로 1을 return합니다.
이로써 find 메서드를 통해 1이라는 집합을 구할 수 있습니다.
그러나 5의 집합을 구해야하는 과정이 무수히 많다면 이러한 재귀호출을 계속하기엔 비효율적입니다.
여기서 우리는 좌표 압축(Path Compression)이라는 기술을 활용하여 이러한 과정을 효율적이게 만들어줄 수 있습니다.
find 메서드 + 좌표 압축
처음 find 메서드는 아래와 같습니다.
static int find(int x) {
if(parent[x] == x) return x;
return find(parent[x]);
}그저 재귀의 값을 리턴하기만 하는 것을 볼 수 있습니다. 여기서 return되는 값을 활용해 parent배열을 갱신하는 것이 좌표 압축이라고 할 수 있습니다.
코드는 아래와 같습니다.
static int find(int x) {
if(parent[x] == x) return x;
return parent[x] = find(parent[x]); //정점 x의 루트를 갱신
}
좌표 압축을 추가한 코드를 통해 다시 find(5) 메서드를 수행해보겠습니다.
좌표압축을 추가한 find(5)를 수행하면
- parent[5]에는 4가 입력되있으므로 find(4)를 다시 호출합니다.
- parent[4]에는 1이 입력되있으므로 find(1)을 다시 호출합니다.
- parent[1]에는 자기 자신이 루트로 기록되있으므로 1을 return합니다.
- parent[4] = 1이 기록되고, 1을 return합니다.
- parent[5] = 1이 기록되고, 1을 return합니다.
이로써 find 메서드를 통해 1이라는 제대로 된 집합을 구할 수 있을 뿐더러, parent배열을 갱신함으로써 재탐색 효율을 크게 올릴 수 있는 것을 확인할 수 있습니다.
정리
이번 시간을 통해 유니온 파인드와 좌표압축을 통한 효율성에 대해 알아볼 수 있었습니다.
유니온 파인드를 검색하면 대부분 좌표압축을 추가한 코드가 나오기 때문에 그냥 외우려면 외울 수 있었는데요.
그러나 학습을 하면서 왜 좌표압축을 사용하지 않으면 안되고, 이해한대로 union 메서드를 통해 집합 탐색을 하고 문제를 풀이했는데 풀리지 않는건지 의문이 생겼습니다.
평소에도 이러한 궁금증이 생기면 매몰되버리기도 하고, 예제가 없는 이해는 없다라고 생각을 하는 편이라 찾는데 조금 시간이 많이 걸렸는데요.
이렇게 궁금증을 가지고, 해결해나가며 학습을 하면 웬만하면 길게 머리속에 남더라구요.
마지막으로 추천하는 문제 2개 올리며 마치도록 하겠습니다. 읽어주셔서 감사합니다.
'CS > 알고리즘' 카테고리의 다른 글
| BFS? Dijkstra? (0) | 2025.01.31 |
|---|---|
| [PS] 백준3584: 가장 가까운 공통 조상 (Java) (0) | 2025.01.12 |
| [TIL] 다익스트라 : 가중치로 0이 들어온다면 (0) | 2024.11.23 |
| [PS] 백준3109 : 빵집 (Java) (0) | 2024.11.22 |
| 다이나믹 프로그래밍(DP) 접근법 및 풀이 전략 (3) | 2024.10.31 |

개발 기술 블로그, Dev
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!

![[PS] 백준3584: 가장 가까운 공통 조상 (Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FR9xiR%2FbtsLLTUpnfD%2FAAAAAAAAAAAAAAAAAAAAACnNaQxx7Oh4k0lH2_3-LrKUNjbX7zwL39WAUPXed0QV%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DN5x%252FgWtjdwWMsVinu11uiLjP4b0%253D)