![[알고리즘] 데이크스트라(Dijkstra)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FJEJJD%2FbtsBGkIePKO%2FAAAAAAAAAAAAAAAAAAAAADrG8ugivjU4BD2_ci5s29W5fPlFWTVhX0ip7-Jf4Igo%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3D4dojl%252FLEBt9%252BHxDXfUkF1IBN8wk%253D)

[알고리즘] 데이크스트라(Dijkstra)CS/알고리즘2023. 12. 9. 18:27
Table of Contents
Intro
어떤 정점으로부터 모든 정점들로의 최단 경로를 구하는 문제는 최단 경로 알고리즘을 적용해서 정해를 구할 수 있다.
이 때 사용되는 최단 경로 알고리즘으로는 아래와 같다.
- 다익스트라(Dijkstra) 알고리즘
- 벨만-포드(Bellman-Ford) 알고리즘
- 플로이드-워셜(Floyd-Warshall) 알고리즘
아래 표는 최단 경로 알고리즘 3가지의 각 차이점에 대해 참고할 수 있도록 생성형 AI를 통해 생성한 자료
| 구분 | 다익스트라(Dijkstra) | 벨만-포드(Bellman-Ford) | 플로이드-워셜(Floyd-Warshall) |
| 목적 | 단일 출발점에서 다른 모든 정점까지의 최단 거리 | 단일 출발점에서 다른 모든 정점까지의 최단 거리 | 모든 정점 쌍 간 최단 거리 |
| 음수 가중치 | ❌ 불가능 (음수 간선 있으면 오동작) | ✅ 가능 | ✅ 가능 |
| 음수 사이클 탐지 | ❌ 불가능 | ✅ 가능 | ✅ 가능 (응용 가능) |
| 시간 복잡도 | O(E log V) (우선순위 큐 사용 시) | O(VE) | O(V³) |
| 공간 복잡도 | O(V + E) | O(V + E) | O(V²) |
| 그래프 유형 | 가중치가 양수인 방향/무방향 그래프 | 방향 그래프 (음수 간선 가능) | 방향 그래프 (모든 쌍) |
| 사용 예시 | 네비게이션, 네트워크 라우팅 | 환율 계산, 음수 사이클 탐지 | 경로 테이블 계산, 전체 최단 거리 미리 계산 |
각 알고리즘에 대해 세부적인 원리에 대해 개별 포스팅으로 정리해보기로 하고, 이번 포스팅에서는 벨만-포드 알고리즘에 대해 작성해보려한다.
INDEX
| 다익스트라(Dijkstra) 알고리즘 포스팅 (현재) |
| 벨만-포드(Bellman-Ford) 알고리즘 포스팅 |
| 플로이드-워셜(Floyd-Warshall) 알고리즘 포스팅 |
Concept
- 그리디 알고리즘의 한 분류
- 다이나믹 프로그래밍 메모이제이션 기법 활용
- 부분 문제 : 한 정점까지의 최단거리는 방문하는 여러개의 정점들의 최단거리로 이루어져있음.
- 주어지는 그래프에서 시작 정점으로부터 각 정점까지의 최단경로를 찾는 알고리즘
Feature
우선순위 큐와 거리배열(DP)을 활용하여 로직 구성.
- 한 정점 V까지의 최단거리를 구할 때 V까지로 가는 여러 정점들의 최단 거리 정보를 활용한다는 특징을 가짐.
- 가중치를 가진 그래프에서 최단거리를 구할 때 쓰이는 알고리즘
- 음수 가중치를 가진 그래프에서는 사용불가.
- 우선순위 큐를 활용함으로써 시간복잡도 : O(N * NlogN)
Implement
인접 리스트를 통한 구현
- 우선 데이크스트라 소스코드를 보자.
private static int dijkstra(int start, int end) {
PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1] - o2[1];
}
});
int[] dp = new int[list.size()]; //거리 저장 배열
Arrays.fill(dist, Integer.MAX_VALUE);
pq.offer(new int[]{start,0});
while(!pq.isEmpty()) {
int[] cur = pq.poll();
if(cur[0] == end) return cur[1]; //목표 정점에 도착한 경우
for(Node n : list.get(cur[0])) {
if(dp[n.v] > cur[1]+n.w) { //기존의 최단거리보다 더 낮을 경우에만
pq.offer(new int[]{n.v, cur[1] + n.w});
dp[n.v] = cur[1]+n.w;
}
}
}
return -1; //start -> end 까지의 경로가 존재하지 않을 경우
}
코드 설명
- 위 코드는 start → end까지의 최단거리를 구하기 위해 두 개의 매개변수를 받아 구현.
- start로부터 모든 정점까지의 최단거리를 구하려면 if(cur[0] == end) return cur[1]; 구문만 제거하면 됨.
- 우선순위 큐의 거리(cur[1])에 따른 오름차순 정렬 재정의
- 거리배열(dp)를 정점의 개수만큼 선언 및 최대값으로 초기화
- while문을 돌면서 큐에서 꺼낸 정점과 인접해있는 정점들에 대해 dp배열의 거리와 비교해 더 최단거리일 경우에만 큐에 추가 및 dp배열 갱신
동작과정

- 위와 같은 그래프에서 1 → 3으로 가는 최단거리는 6
- 1 → 3 (거리 : 10)
- 1 → 2 → 4 → 3 (거리 : 3+1+2 = 6)

- 1번 정점과 인접한 2(거리:3) 와 3(거리:10)이 큐에 추가되고 dp배열 갱신이 이루어짐.
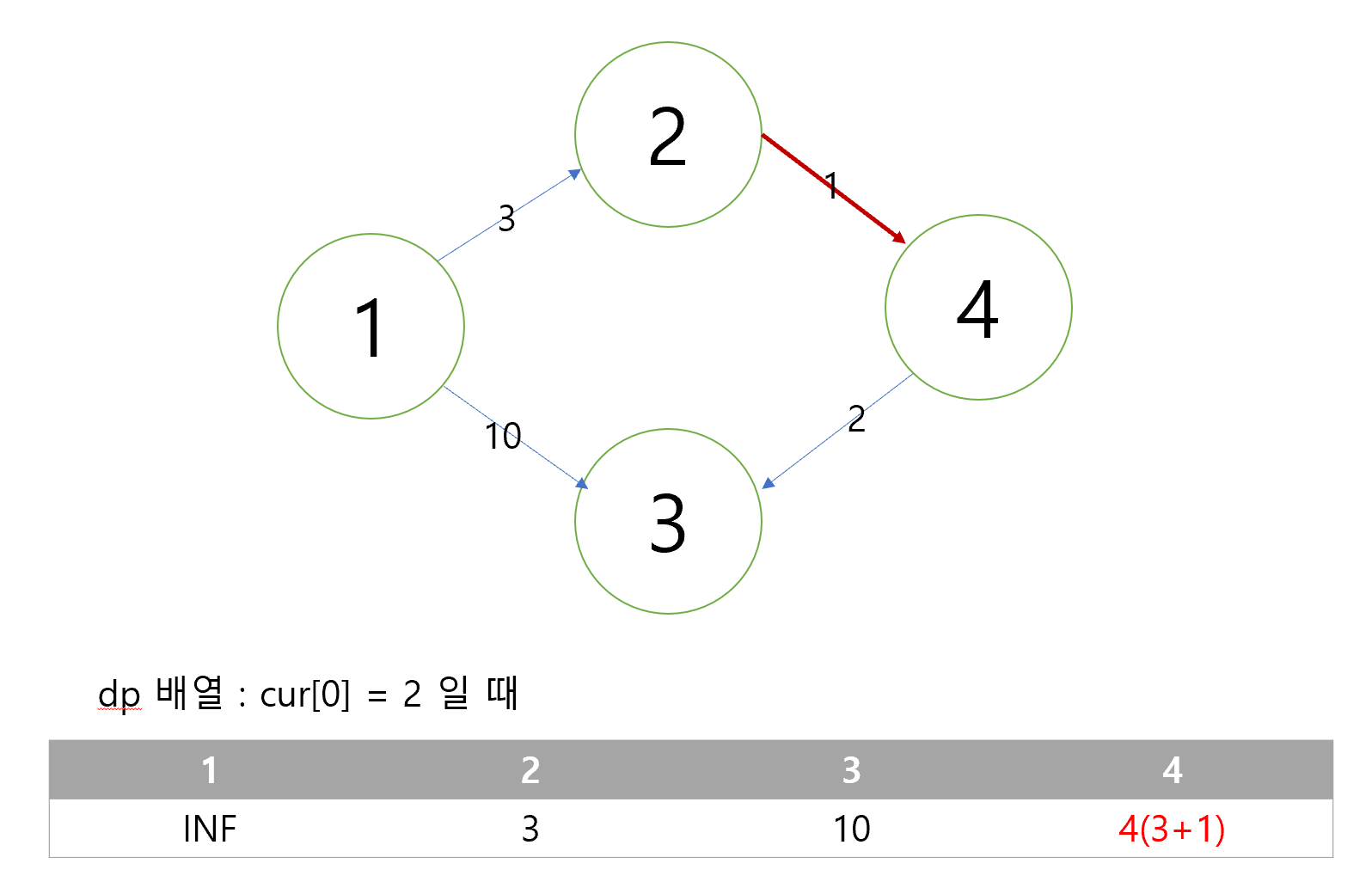
- 우선순위 큐 정렬에 의해 2번 정점이 먼저 꺼내지고 인접한 4번 정점이 큐에 추가되고(거리:4) 최단 거리 갱신이 이루어짐.

- 4번 정점이 큐에서 꺼내질 때 현재 부분문제인 1→4 까지의 최단거리는 4
- 4에서 4→3 까지의 거리인 2를 더해 6과 dp[3]의 값을 비교
- 10(기존값) > 6 이므로 dp[3]이 6으로 갱신됨.
정리
- 데이크스트라는 알고리즘 문제 중에서 꽤나 비중있는 알고리즘 분류 중 하나이며 생각보다 개념이 쉽기 때문에 한번 제대로 알아두면 두고두고 써먹을 수 있는 알고리즘이니 정리를 한번 해보는것도 나쁘지 않음.
- 간단히 요약하자면 BFS를 알고있는 사람이라면 BFS의 PQ(우선순위 큐)버전이라 생각하는 것도 좋을 듯!
(약간의 dp를 곁들인)
+ 추가 (25.02.02)
최근 다익스트라 알고리즘을 다시 공부하며 궁금한 점이 있어 새롭게 정리해보았다.
항상 다익스트라를 구현할 때 습관적으로 dist라는 거리 배열을 통해서 분기 처리를 진행했었다.
그러나 다익스트라의 특징을 다시 생각해보면 현재 방문한 정점에 대해서 최단거리임이 보장되기 때문에 일반적인 boolean 방문 체크로도 되어야하지 않을까? 라는 생각이 들었다.
(물론 각 정점까지의 모든 거리를 구할 필요가 없다는 전제에서..)
이렇게 생각한 이유는 다익스트라의 경우 시작 정점에서 인접한 모든 정점에 대해 탐색을 진행한다.
또한 우선순위 큐를 통해 최소 비용에 대해 먼저 탐색을 진행하게 된다. 이는 곧 현재 도착한 정점에 대해서 최소 비용이라는 명제가 됨.
만약 모든 정점까지의 거리를 구할 필요가 없이 단순히 두 정점 사이의 최단 거리를 구하기만 하면 된다면 거리 배열이 아닌 boolean 방문 배열을 사용해 보는것도 좋을 것 같다.
static int Dijkstra() {
PriorityQueue<Node> pq = new PriorityQueue<>((o1,o2) -> o1.w - o2.w);
pq.offer(new Node(start, 0));
boolean[] v = new boolean[N+1];
while(!pq.isEmpty()) {
Node cur = pq.poll();
v[cur.v] = true;
if(cur.v == end) return cur.w;
for(Node next : list.get(cur.v)) {
if(v[next.v]) continue;
pq.offer(new Node(next.v, cur.w + next.w));
}
}
return -1;
}'CS > 알고리즘' 카테고리의 다른 글
| [PS] 백준13460 : 구슬 탈출 2(Java) (0) | 2023.12.13 |
|---|---|
| [PS] 백준2294 : 동전 2(Java) (0) | 2023.12.09 |
| [알고리즘] 최장 증가 수열 (LIS, Longest Increasing Subsequence) (0) | 2023.12.08 |
| [PS] 백준20165 : 인내의 도미노 장인 호석(Java) (0) | 2023.12.08 |
| [알고리즘] 배낭 문제(Knapsack Problem) (0) | 2023.12.08 |

@Beemo9 :: BeHinD
개발 기술 블로그, Dev
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[PS] 백준13460 : 구슬 탈출 2(Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fbd8hnP%2FbtsBRPvgr6V%2FAAAAAAAAAAAAAAAAAAAAAI2XbCeMSyX8DYQk4nnKPIwAXdLpGYeBjULtaRO9JCpr%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DQiqtt4I%252FD3QDcfE6NfmYqMaI%252FFE%253D)
![[PS] 백준2294 : 동전 2(Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbW1KbI%2FbtsBJbRaJEa%2FAAAAAAAAAAAAAAAAAAAAAKUVEQf5Zh3niFYGYFD6XOYsIoIczMxeu1r1pt-U0FNE%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3Db3i6kCMyFXLQ2fFW%252FXsT43TyRTI%253D)
![[알고리즘] 최장 증가 수열 (LIS, Longest Increasing Subsequence)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fbhhomz%2FbtsBFnZlrIz%2FAAAAAAAAAAAAAAAAAAAAANiM93j9fYPg7yEzXFs0yz03DGC39V1JHfOVUYyGcHzh%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3D4j88tz%252FX%252BQB6r8RtKR2KFRkpPkE%253D)
![[PS] 백준20165 : 인내의 도미노 장인 호석(Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FsE4mw%2FbtsBxUYk39R%2FAAAAAAAAAAAAAAAAAAAAAMH3n2b42cnW19m3Ton4xA8hx5MZ-_DA-RpFMipKlHwP%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1774969199%26allow_ip%3D%26allow_referer%3D%26signature%3DFSutedH%252FP2hh34I65OW1rQxjlYA%253D)