![[PS] 백준2003 : 수들의 합 2(JAVA) - 투 포인터 활용편](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FdbqT83%2FbtsF0uAVdCZ%2FAAAAAAAAAAAAAAAAAAAAAFHZDKCAGYTQzaZDHxt1Z1cJIEnDU79bXiZzUsEMoCpE%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DSQ6AnEXC7oLvyQ9hpHobW1%252F2wZY%253D)

문제
https://www.acmicpc.net/problem/2003
2003번: 수들의 합 2
첫째 줄에 N(1 ≤ N ≤ 10,000), M(1 ≤ M ≤ 300,000,000)이 주어진다. 다음 줄에는 A[1], A[2], …, A[N]이 공백으로 분리되어 주어진다. 각각의 A[x]는 30,000을 넘지 않는 자연수이다.
www.acmicpc.net
풀이
투 포인터를 활용
Solving
문제에서 주어지는 수열에서 구간합이 M이 되는 조합의 경우의 수를 구하는 문제입니다.
그리디하게 접근하여 풀이를 하게되면 2중 for문으로 시간복잡도가 O(N^2)이 됩니다.
그리디한 풀이는 다음과 같습니다.
- 각 수열의 i번째 원소에서부터
- i+1번 이후의 수열을 누적
- 누적합이 M이 되면 카운트
본격적으로 투 포인터를 사용하게 되면 O(N^2)의 시간복잡도를 O(N)으로 줄일 수 있습니다.
다음은 투 포인터를 활용하여 접근하는 과정에 대한 설명입니다.
이번 풀이에서 재미있던 부분은 투 포인터의 경우 대부분 L=0, R=arr.length에 두고 시작하지만 해당 풀이에선 시작지점에서부터 출발하여 구간합을 구할 수 있다는 부분입니다.
수행과정

구간합을 구하는 문제로써 두 개의 포인터 L(eft)과 R(ight)는 0에서부터 출발합니다.
구간합을 나타내는 sum의 값이 M보다 작다면 이는 곧 추가적인 수가 필요하다는 이야기이므로 R의 포인터를 이동시켜줍니다.
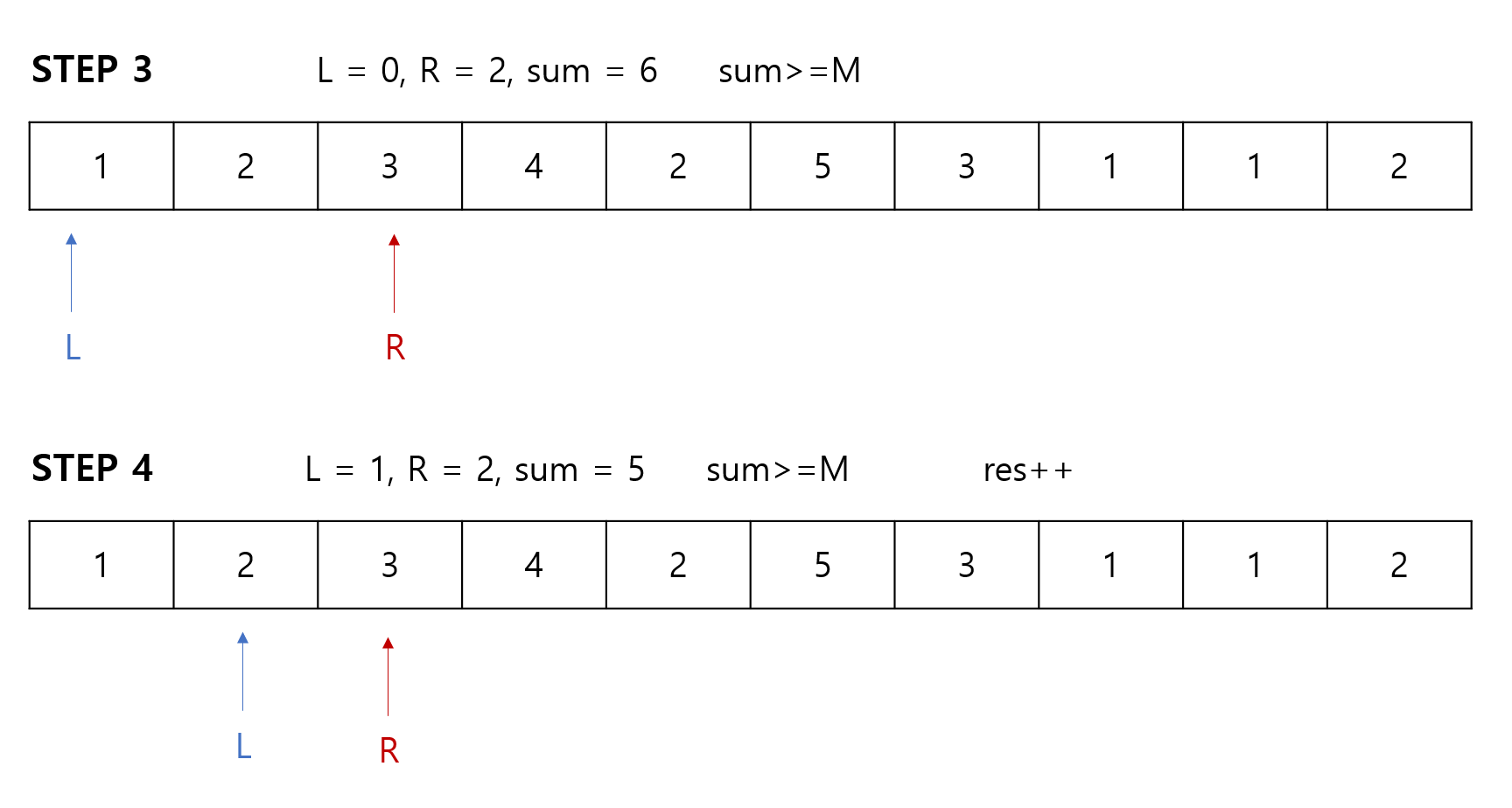
(STEP3) sum의 값이 M보다 (같거나)크다면 이는 곧 감소하는 수가 필요하다는 이야기입니다.
그러므로 기존 수열의 L값을 sum에서 빼고, L포인터를 이동합니다.
만약 구간합(sum)이 M과 같다면 카운팅을 하고, L포인터를 우측으로 이동합니다.
L포인터를 움직이는 이유는 STEP3의 이유와 같습니다.
다음으로 전체 진행과정에 대한 이미지입니다.







포인터의 이동 과정에서 만약 R포인터가 배열의 길이보다 커지게 되면 함수는 종료됩니다.
R포인터가 이동하게 되는 이유는 L ~ R의 구간합이 M보다 낮다는 이야기이므로,
L포인터를 이동하여 구간합을 구해도 여전히 구간합은 M보다 낮기에 추가적인 계산이 필요없습니다.
소스코드
혹시몰라 두 가지에 대한 각각의 소스코드를 첨부했습니다.
백준에서 두 가지 풀이로 제출을 해보면 시간복잡도가 크게 차이가 난다는걸 알 수 있습니다.
그리디한 풀이 O(N^2)
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
//BOJ_2003 수들의 합 2
public class Main {
static int N, M;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken()); //수열의 개수
M = Integer.parseInt(st.nextToken()); //타겟 넘버
int[] arr = new int[N];
st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int res = 0;
for(int i=0; i<N; i++) {
int sum = arr[i];
if(sum == M) {
res++;
continue;
}
for(int j=i+1; j<N; j++) {
sum += arr[j];
if(sum == M) {
res++;
break;
}
else if(sum > M) break;
}
}
System.out.println(res);
}
}
투 포인터 풀이 O(N)
import java.io.*;
import java.util.StringTokenizer;
//BOJ_2003 수들의 합 2
public class Main {
static int N, M;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken()); //수열의 개수
M = Integer.parseInt(st.nextToken()); //타겟 넘버
int[] arr = new int[N];
st = new StringTokenizer(br.readLine());
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
int res = 0;
int l,r,sum;
l = r = sum = 0;
//같은 위치에서 시작
while(true) {
if(sum >= M) {
sum -= arr[l++];
}
else if(r==N) break;
else { //sum < M
sum += arr[r++];
}
if(sum == M) {
res++;
}
}
System.out.println(res);
}
}
정리

여담으로..
이번에 N기업의 코딩테스트를 진행하며 투 포인터로 풀이를 했다면 정말 좋았을텐데!... 라고 후회했던 문제가 있었습니다.
해당 문제의 풀이를 저는 LIS 이분탐색을 통해 풀이를 하려다 실수를 했지만 만약 투 포인터 접근이 생각이 났더라면 수월하게 풀이를 할 수 있었을 것 같아 너무 아쉬움이 남은 경험이였습니다.
다음에도 비슷한 문제가 나올 수 있을 것 같아 투 포인터에 대한 개념 정리 및 저만의 무기로 만들고자 풀이했던 백준 실버 문제로 역시나 처음부터 그리디한 풀이를 한 뒤 투 포인터로 접근하려했지만 분류를 알고 있음에도 구현하지 못해 레퍼런스를 보고 풀이를 했습니다.
아직 투 포인터에 대한 활용도가 많이 부족하다는 걸 깨닫고 그래프 탐색만 풀지않고 이러한 시간복잡도를 줄여주는 알고리즘들을 많이 공부해야겠다 느꼈습니다!...
'CS > 알고리즘' 카테고리의 다른 글
| [코드트리 조별과제] 3주차 학습 (0) | 2024.07.30 |
|---|---|
| [PS] 백준1967 : 트리의 지름(Java) (0) | 2024.06.01 |
| [PS] 백준2143 : 두 배열의 합(Java) (0) | 2024.02.28 |
| [PS] 백준2211 : 네트워크 복구(Java) (0) | 2024.02.27 |
| [PS] 백준 2141 : 우체국(JAVA) (0) | 2024.02.27 |

개발 기술 블로그, Dev
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[코드트리 조별과제] 3주차 학습](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FkBs3x%2FbtsIQyGMAnt%2FAAAAAAAAAAAAAAAAAAAAAAx5coQEhwxICC2nqC1E2yKCrP82Vm5wH0TJgqdDAKDr%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DzPxDQH%252BX9gtKaXn6UkKwDOM9LTk%253D)
![[PS] 백준1967 : 트리의 지름(Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fb580Z1%2FbtsHLUXeEWF%2FAAAAAAAAAAAAAAAAAAAAAGm-5JLUcanenfB6erXxnDc-7eGR2RkmSlVNA8tGAbDq%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DSRmHEYxP0R0mitzTUiCo32gKmd8%253D)
![[PS] 백준2143 : 두 배열의 합(Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbQiOW7%2FbtsFkHN8A31%2FAAAAAAAAAAAAAAAAAAAAAM0-_kRfjTNe9tYBI6JLVrizWViNzH_tIQv05-CPA-lv%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3Dh2POHFqnIKRIQ2led9crTS0KtPM%253D)
![[PS] 백준2211 : 네트워크 복구(Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fds5BsU%2FbtsFhf5I31q%2FAAAAAAAAAAAAAAAAAAAAAFMvhhqR0AIBxIx7c-eE8ffdaTLrHXPmDEegLrRewxnw%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3D%252FMmabGdT1SxeVMWzsRfeexHF%252B4g%253D)