![[PS] 백준17485 : 진우의 달 여행 (Large)(Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FUNQ1R%2FbtsKgDmtGxV%2FAAAAAAAAAAAAAAAAAAAAAKDINZBbGUwl--sPqQP3uerDthnTYiswjKAhBFi76LaJ%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DJBzoU8O1AFL1MLKA4n4Y1Keuf%252B8%253D)

문제
https://www.acmicpc.net/problem/17485
풀이
다이나믹 프로그래밍 풀이
접근법
처음에는 다익스트라로 최소비용 구하면 되는 것 아냐? 라는 생각을 잠깐 했지만 출발지점이 1000개가 될 수 있기에 DP로 풀었다.
문제 조건
해당 문제에서 각 원소의 위치에서 할 수 있는 행동은 3가지다.
왼쪽 아래
중간
오른쪽 아래
또 다른 조건으로는 이전 행동과 같은 행동을 취하지 못한다.
dp로 풀이를 하기로 했으니 각 원소의 위치의 최선의 값을 어떻게 찾을지 생각하는 것 뿐이다.
간단하게 생각하면 dp[i][j]는 3가지 이전해 + 현재값 중 최소값을 선택하면 될 것으로 보인다.
그러나 다음해를 구하기 위해서 이전해가 어떤 방향에서 진행된 값인지 알 필요가 있다.
이를 위해 3차원 배열로 dp배열을 구성했다. dp[i][j][어디에서 온건지]
그럼 점화식을 다음과 같이 세워볼 수 있다.
dp[i][j][0] = 왼쪽에서 온 해를 의미한다.
dp[i][j][1] = 중간에서 온 해를 의미한다.
dp[i][j][2] = 오른쪽에서 온 해를 의미한다.
즉 각각의 원소의 [0],[1],[2]는 이전에 진행된 방향을 의미한다.
그럼 이제 해를 구할 때는 어떻게 할까?
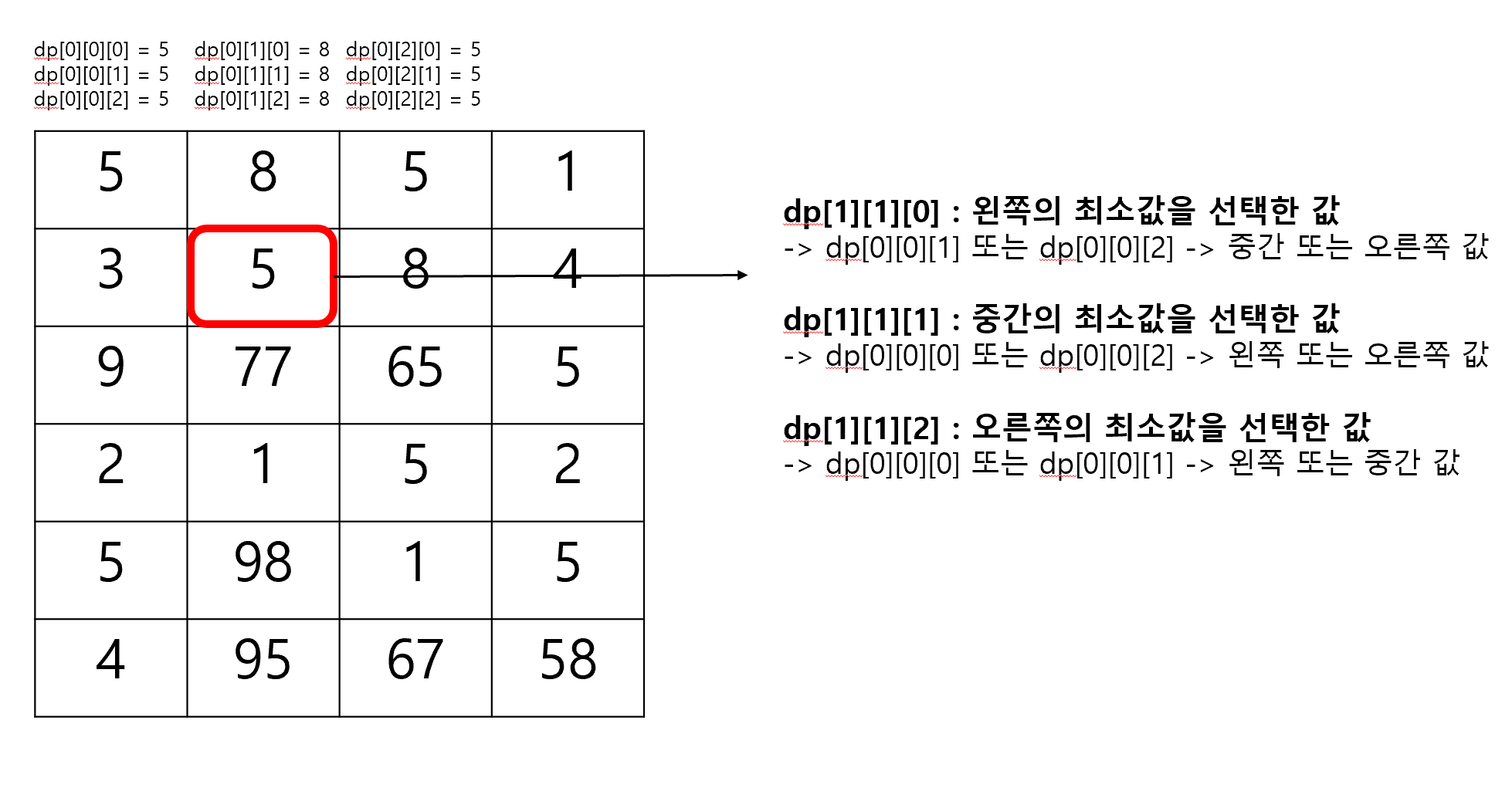
현재 i,j의 해를 3가지 방향에 대해서 구해야한다.
- 왼쪽 위 해를 활용한 경우 = dp[i][j][0]
- 중간 위 해를 활용한 경우 = dp[i][j][1]
- 오른쪽 위 해를 활용한 경우 = dp[i][j][2]
1번의 경우 이전해의 0번째 원소(dp[i-1][j-1][0])를 비교해선 안된다. 이유는 왼쪽에서 진행되었던 값을 통해 왼쪽으로 다시 진행한 값을 구한다면 조건을 위반하기 때문이다. 나머지 방향에 대해서도 동일한 조건을 적용하면 해를 구할 수 있다.
이 로직을 토대로 소스코드를 구현해보자.
소스코드
import java.io.*;
import java.util.StringTokenizer;
//BOJ_17485
public class Main {
static int N, M, res;
static int[][] map;
static int[][][] dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
map = new int[N][M];
for(int i=0; i<N; i++) {
st = new StringTokenizer(br.readLine());
for(int j=0; j<M; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
}
}
/**
* BFS 풀이의 경우 시작지점 1000개에 대해 각각 돌려야하므로 O(1000 * 1000 * 1000) = 10억으로 시간초과
* 메모이제이션을 통해 i,j에대해 이전 행동에 대한 최소값을 갱신
* 왼쪽위, 위, 오른쪽위
* **/
dp = new int[N][M][3]; //3가지 움직임에 대한 3차원 배열
for(int i=0; i<M; i++) { //시작점 초기화
dp[0][i][0] = map[0][i];
dp[0][i][1] = map[0][i];
dp[0][i][2] = map[0][i];
}
for(int i=1; i<N; i++) {
for(int j=0; j<M; j++) {
if (j == 0) {
dp[i][j][0] = 10000000;
dp[i][j][1] = Math.min(dp[i-1][j][0] + map[i][j], dp[i-1][j][2] + map[i][j]);
dp[i][j][2] = Math.min(dp[i-1][j+1][0] + map[i][j], dp[i-1][j+1][1] + map[i][j]);
}
else if(j == M-1) {
dp[i][j][0] = Math.min(dp[i-1][j-1][1] + map[i][j], dp[i-1][j-1][2] + map[i][j]);
dp[i][j][1] = Math.min(dp[i-1][j][0] + map[i][j], dp[i-1][j][2] + map[i][j]);
dp[i][j][2] = 10000000;
}
else {
dp[i][j][0] = Math.min(dp[i-1][j-1][1] + map[i][j], dp[i-1][j-1][2] + map[i][j]);
dp[i][j][1] = Math.min(dp[i-1][j][0] + map[i][j], dp[i-1][j][2] + map[i][j]);
dp[i][j][2] = Math.min(dp[i-1][j+1][0] + map[i][j], dp[i-1][j+1][1] + map[i][j]);
}
}
}
res = Integer.MAX_VALUE;
for(int i=0; i<M; i++) {
for(int j=0; j<3; j++) {
res = Math.min(res, dp[N-1][i][j]);
}
}
System.out.println(res);
}
}
정리
조건이 굉장히 3차원 배열을 써달라는 느낌의 조건이여서 쉽게 3차원 배열 메모이제이션을 수행했던 것 같다.
DP를 풀 때 보통 각 원소의 최적값을 선택하는 점화식을 떠올리는 것으로 빠르게 풀이하는 편이다.
그러나 이번에 정리를 하면서, 직감대로 풀이를 해서 그런지 설명을 하려고하니 쉽게 정리가 되지 않더라.
PPT에 하나씩 흐름 정리를 하다보니 겨우 이해한 느낌이랄까… 누군가에게 설명한다는 것은 늘 쉬운것같지만 어렵다는걸 또한번 느꼈다.
'CS > 알고리즘' 카테고리의 다른 글
| [PS] 백준3109 : 빵집 (Java) (0) | 2024.11.22 |
|---|---|
| 다이나믹 프로그래밍(DP) 접근법 및 풀이 전략 (3) | 2024.10.31 |
| [PS] 프로그래머스 Lv4 : 도둑질(Java) (0) | 2024.10.14 |
| [PS] 백준3020 : 개똥벌레(Java) (0) | 2024.10.10 |
| [PS] 백준1339 : 단어 수학(Java) (0) | 2024.10.07 |

개발 기술 블로그, Dev
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!

![[PS] 백준3020 : 개똥벌레(Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2F5XwZV%2FbtsJ16grjx4%2FAAAAAAAAAAAAAAAAAAAAAM7GrIIR3fH36lH--nZ1vUZzl0CS1fUiXpUn_5GCtEH5%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DEJtyr0oGfsntv5%252BUaO%252BG0DnY9nI%253D)