![[코드트리 조별과제] 4주차 학습 (정렬 알고리즘)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FzCFDu%2FbtsIZvjnz8Z%2FAAAAAAAAAAAAAAAAAAAAACucsow92wFN3L7BDiN5aYwmel-IN7hPX71fQTqMqR3c%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3Dif1m2AKwKOT45cUrFlh%252B0mkT48o%253D)

Intro
코드트리 조별과제를 진행한지 저에겐 2주차가 되는 시점이네요!
이번 주차에는 평소 해야지 해야지... 하고 생각만 하던 정렬 알고리즘에 대해 학습을 진행했습니다.
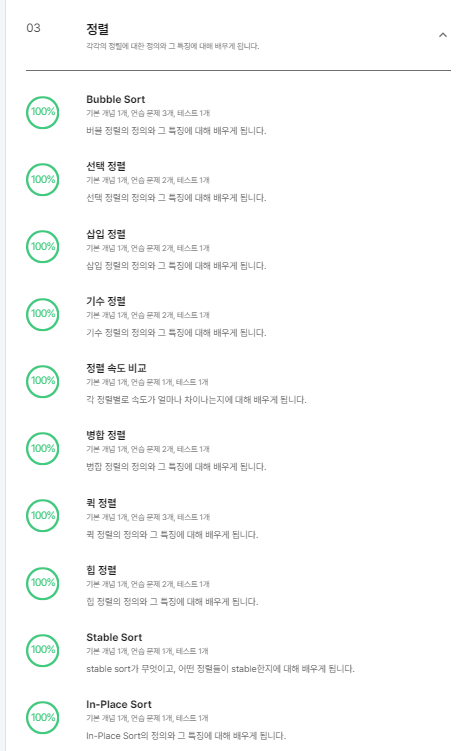
보다시피 코드트리에는 정렬 알고리즘 학습 커리큘럼이 잘 구성이 되어있고, 이미지 및 영상 참고자료도 보기 편하게 제공이 되어 원활하게 학습할 수 있었습니다. 또한 각각의 알고리즘 동작 방식과 시간, 공간 복잡도를 중점으로 학습하였습니다.
Bubble Sort(버블 정렬)
거품 정렬은 가장 단순한 정렬 알고리즘입니다. 기본적인 아이디어는 간단합니다. 첫번째와 두번째 값을 비교하고, 두번째와 세번째 값을 비교하고, ... n-1번째와 n번째 값을 비교합니다. 이 과정에서 순서가 맞지 않은 값을 서로 교환해줍니다. 이런 절차를 정렬이 될 때 까지 반복합니다.

코드를 작성하는 것은 어렵지 않지만, 상당히 비효율적인 알고리즘이기 때문에, 성능이 다른 알고리즘에 비해 좋지 않다는 단점이 있습니다.
시간복잡도 -> O(N^2) (단, 이미 정렬된 배열의 경우 O(N))
메모리의 경우 N길이의 1차원 배열 외 추가적인 메모리 소비는 없습니다.
Code
import java.io.*;
import java.util.*;
//Code Tree
public class Main {
static int N;
static int[] arr;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
arr = new int[N];
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
// Bubble Sort Code Start
boolean sorted = false;
while(!sorted) {
sorted = true;
for(int i=0; i<N-1; i++) {
if(arr[i] > arr[i+1]) {
int temp = arr[i];
arr[i] = arr[i+1];
arr[i+1] = temp;
sorted = false;
}
}
}
// Bubble Sort Code End
for(int idx : arr) sb.append(idx).append(" ");
System.out.println(sb);
}
}
선택 정렬
선택 정렬의 주요 아이디어는 다음과 같습니다.
1. 전체 값 중 가장 작은 값을 찾음
2. 해당 값을 맨 첫번째에 배치함
3. 첫번째 값을 제외하고 가장 작은 값을 찾아 두번째에 배치함
4. 두번째, 세번째, ... n-1번째 값을 제외하고 가장 작은 값을 찾아 정해진 위치에 배치함.

시간복잡도 -> O(N^2) (이미 정렬이 되어 있다고해도 무조건 순회를 합니다.)
메모리의 경우 N길이의 1차원 배열 외 추가적인 메모리 소비는 없습니다.
Code
import java.io.*;
import java.util.*;
//Code Tree
public class Main {
static int N;
static int[] arr;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
arr = new int[N];
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
for(int i=0; i<N-1; i++) {
int min = i;
for(int j=i+1; j<N; j++) {
if(arr[min] > arr[j]) {
min = j;
}
}
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
for(int idx : arr) sb.append(idx).append(" ");
System.out.println(sb);
}
}
삽입 정렬
앞에서부터 순서대로 보면서 앞에 있는 모든 원소가 정렬이 되어 있다는 가정 하에서 현재 원소의 위치를 적절하게 집어넣는 정렬입니다.

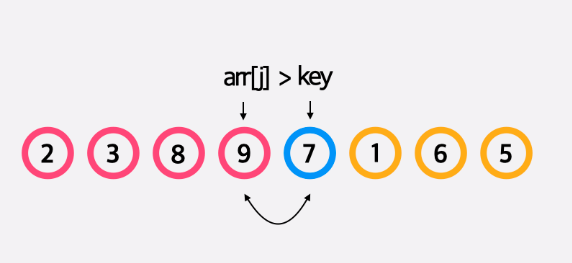
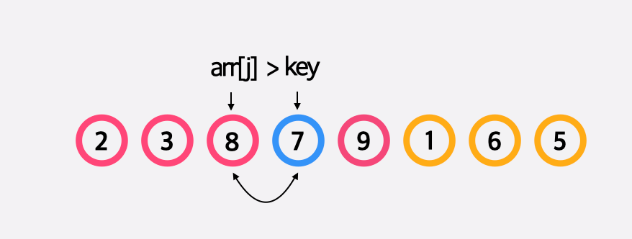
n개의 원소에 대해 값 삽입을 수행해야 하는데, 2번째 원소의 경우엔 최대 1개의 원소를 이동해야 하고, 3번째 원소의 경우엔 최대 2개의 원소를 이동해야 하며, n번째 원소까지 삽입하는 경우엔 최대 n−1개의 원소가 이동해야 하므로 결과적으로 최대 n(n−1)/2 개의 원소가 이동해야합니다.
시간복잡도 -> O(N^2)
메모리의 경우 N길이의 1차원 배열 외 추가적인 메모리 소비는 없습니다.
Code
import java.io.*;
import java.util.*;
//Code Tree
public class Main {
static int N;
static int[] arr;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
arr = new int[N];
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
for(int i=1; i<N; i++) {
int j = i-1;
int key = arr[i];
while(j>=0 && arr[j] > key) {
arr[j+1] = arr[j];
j--;
}
arr[j+1] = key;
}
for(int idx : arr) sb.append(idx).append(" ");
System.out.println(sb);
}
}
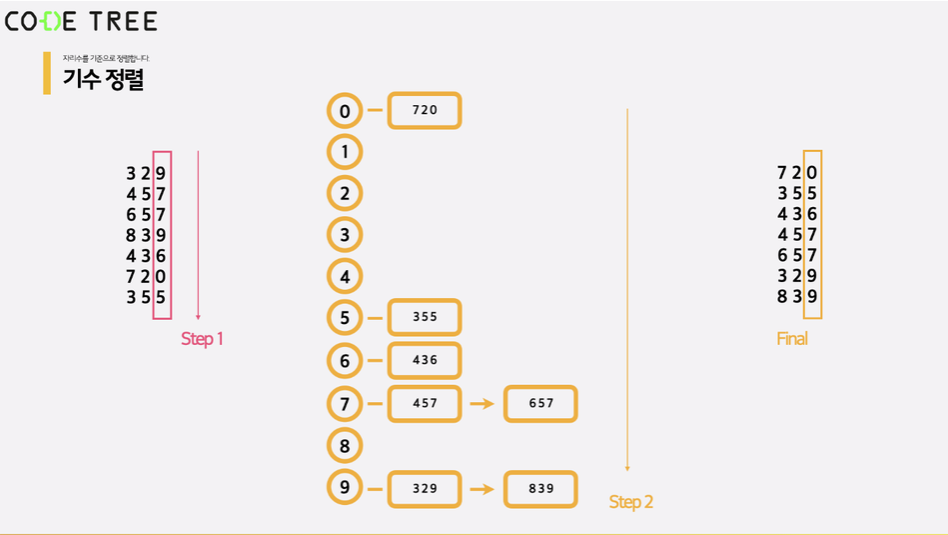
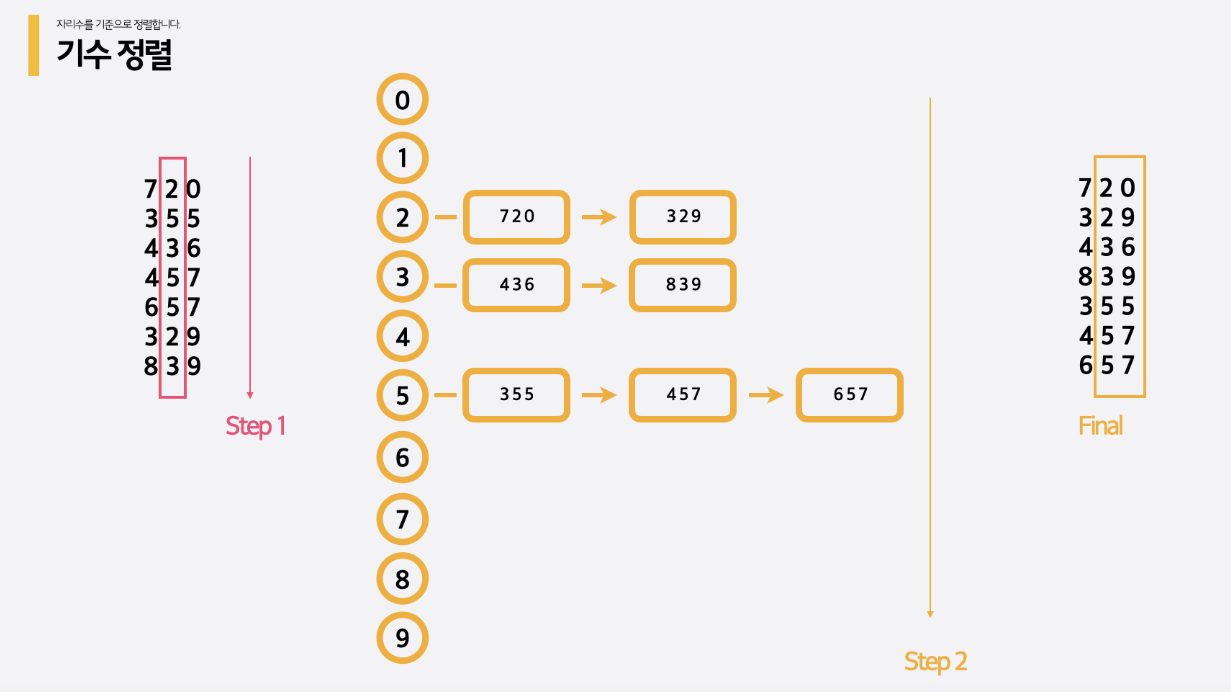
기수 정렬
기수정렬의 경우 O(k*N)이라는 시간복잡도를 가지며, k의 경우 원소 자리수를 의미합니다.
기수 정렬은 맨 뒤에 있는 자릿수 부터 해당 자리수를 기준으로 정렬한 뒤, 점점 앞으로 이동하며 각 자리수를 기준으로 정렬하다가 최종적으로 가장 높은 자리수를 기준으로 정렬하는 방법입니다.
그러므로 주어진 숫자들의 자릿수가 다른 경우, 기수 정렬로 모든 원소를 정렬할 수는 없습니다.
소수는 적용 불가능
기수만큼의 추가 메모리 공간이 필요
LSD와 MSD 방식이 있음
- LSD : 가장 작은 자리수부터 정렬
- MSD : 가장 큰 자리수부터 정렬
Code (LSD IN JAVA)
import java.io.*;
import java.util.*;
//Code Tree
public class Main {
static int N;
static int[] arr;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
arr = new int[N];
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
//자바에서의 기수 정렬?? >> 배열 원소를 연결리스트로 해야한다는건데...
radixsort(arr, arr.length);
for(int idx : arr) sb.append(idx).append(" ");
System.out.println(sb);
}
static int getMax(int arr[], int n) {
int mx = arr[0];
for (int i = 1; i < n; i++) {
if (arr[i] > mx) {
mx = arr[i];
}
}
return mx;
}
// A function to do counting sort of arr[] according to
// the digit represented by exp.
static void countSort(int arr[], int n, int exp) {
int output[] = new int[n]; // output array
int i;
int count[] = new int[10];
Arrays.fill(count, 0);
// Store count of occurrences in count[]
for (i = 0; i < n; i++) {
count[(arr[i] / exp) % 10]++;
}
// Change count[i] so that count[i] now contains actual
// position of this digit in output[]
for (i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
// Build the output array
for (i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// Copy the output array to arr[], so that arr[] now
// contains sorted numbers according to current digit
for (i = 0; i < n; i++) {
arr[i] = output[i];
}
}
// The main function to that sorts arr[] of size n using
// Radix Sort
static void radixsort(int arr[], int n) {
// Find the maximum number to know number of digits
int m = getMax(arr, n);
// Do counting sort for every digit. Note that instead
// of passing digit number, exp is passed. exp is 10^i
// where i is current digit number
for (int exp = 1; m / exp > 0; exp *= 10) {
countSort(arr, n, exp);
}
}
// A utility function to print an array
static void print(int arr[], int n) {
for (int i = 0; i < n; i++) {
System.out.print(arr[i] + " ");
}
}
}
정렬 간 속도 비교
거품, 선택, 삽입 전부 O(N^2)이라는 시간복잡도를 가지지만, 실제 소요되는 시간은 많이 다릅니다.
- 거품 정렬의 경우, 일반적으로 셋 중 가장 느립니다. 그러나 정렬된 배열의 경우, sorted의 값이 계속 true이기 때문에 시간이 매우 빨라집니다.
- 선택 정렬의 경우 배열의 상태와 상관 없이, 1번째로 작은 원소를 찾고, 2번째로 작은 원소를 찾고, ... 하는 과정을 거치기 때문에 어떠한 상황이던 동일한 시간을 보여줍니다.
- 삽입 정렬의 경우 일반적으로는 가장 빠르나, 값이 반대로 정렬되어 있는 경우 성능이 많이 떨어진다는 단점이 있습니다. 또한, 앞 배열에 값을 삽입하는 알고리즘의 특성상 이미 정렬된 배열에 추가적으로 값을 몇개 추가하여 정렬하는 경우에 좋은 성능을 보여줍니다.
이제부터는 O(N^2) 시간복잡도를 벗어난 조금 더 효율적인 정렬에 대해 알아보겠습니다.
병합 정렬
병합 정렬은 배열의 길이가 1개가 될 때 까지 재귀적으로 쪼개기 → 쪼갠 배열을 합쳐가며 정렬된 배열로 만들기 라는 과정을 거치게 됩니다. 이렇게 동일한 문제로 쪼갠 뒤, 다시 합쳐주는 방식을 분할 정복(Divide and Conquer) 이라 부릅니다.
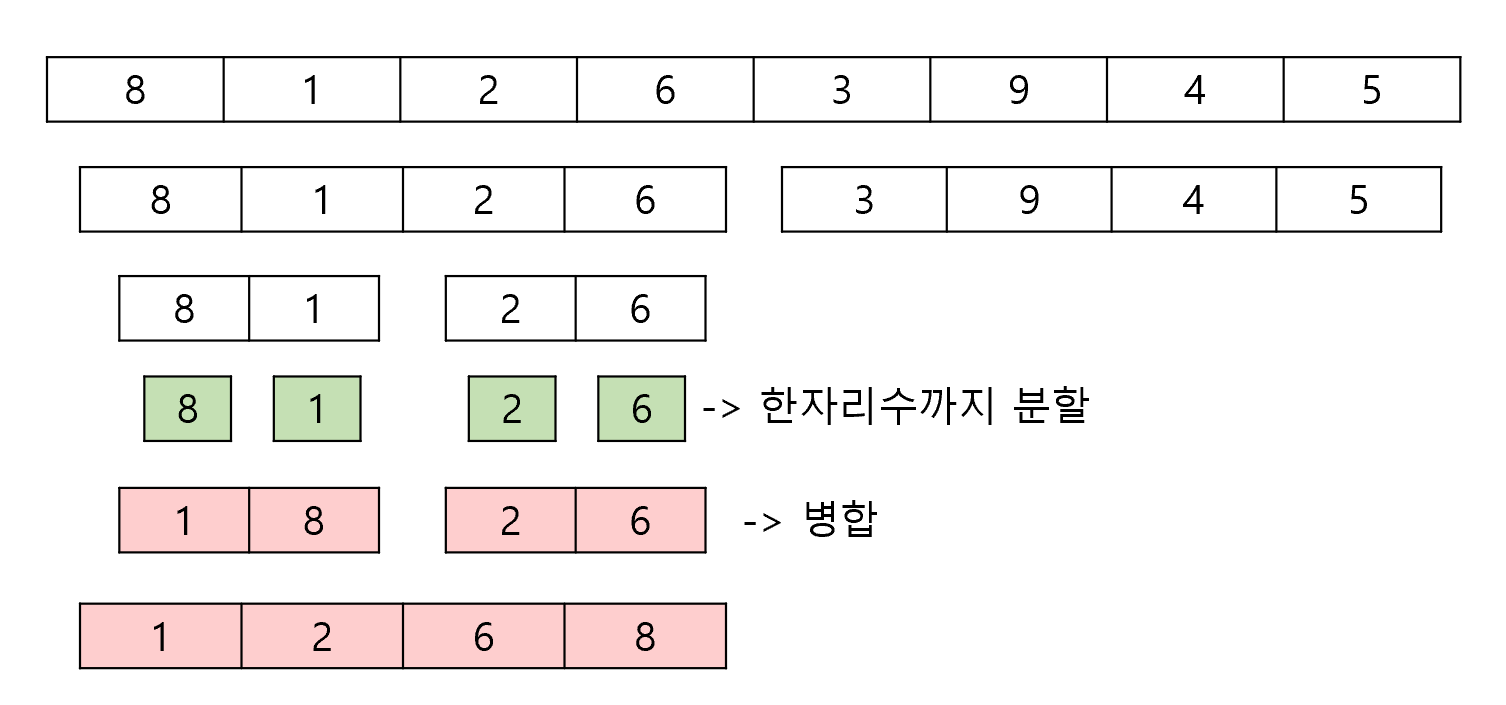
배열 쪼개기 → O(logN)
배열 합치기 → O(N)
총 시간복잡도 O(NlogN)
메모리의 경우 병합 시 필요한 추가적인 N길이의 1차원 배열이 추가로 필요합니다.
Code
import java.io.*;
import java.util.*;
//Code Tree
public class Main {
static int N;
static int[] merged;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
int[] arr = new int[N];
for(int i=0; i<N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
merged = new int[N];
mergeSort(arr, 0, arr.length-1);
for(int i=0; i<N; i++) sb.append(arr[i]).append(" ");
System.out.println(sb);
}
static void mergeSort(int arr[], int low, int high) {
if(low < high) {
final int mid = low + (high-low) / 2;
mergeSort(arr, low, mid);
mergeSort(arr, mid+1, high);
merge(arr, low, mid, high);
}
}
private static void merge(int[] arr, int low, int mid, int high) {
int i = low;
int j = mid+1;
int k = low;
while(i<=mid && j<=high) {
if(arr[i] <= arr[j]) {
merged[k++] = arr[i++];
}
else {
merged[k++] = arr[j++];
}
}
while(i <= mid) {
merged[k++] = arr[i++];
}
while(j <= high) {
merged[k++] = arr[j++];
}
for(int l=low; l<=high; l++) {
arr[l] = merged[l];
}
}
}
퀵 정렬
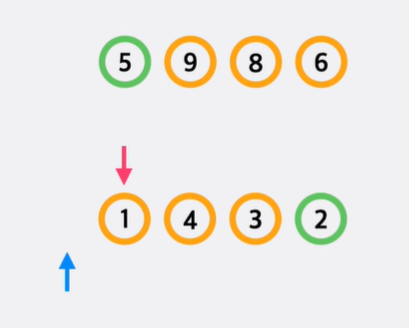
중앙값(피벗)을 선택 후 중앙값을 기준으로 작은값은 왼쪽, 같거나 큰 값은 오른쪽으로 정렬합니다.
옮기는 방식은 현재 pivot인 수보다 같거나 큰 값을 가리키는 포인터(파란색)를 정함과 동시에 왼쪽에서부터 pivot보다 작은 수를 탐색하는 빨간색 포인터를 찾습니다.

파란색과 빨간색 포인터를 찾고나면 두 값을 바꿔줍니다. 이 후 동일하게 빨간색 포인터를 이동하면서 pivot보다 작은 수를 탐색합니다. 탐색이 되면 파란색 포인터를 한칸 우측으로 이동 후 두 값을 교환합니다.
빨간색 포인터가 끝 지점 도달 시, 파란색 포인터 다음 지점과 pivot을 교환해줌으로써 한 번의 정렬이 끝납니다.
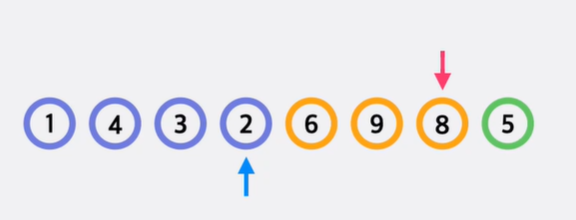
이 후 이동된 pivot을 기준으로 왼쪽, 오른쪽 각 부분에 대해 다시 퀵 정렬을 진행합니다.(분할정복)

시간복잡도의 경우 병합 정렬이 정확히 logN회 분할이 됨과 달리, 퀵 정렬의 최악 경우 N번 분할이 진행되기 때문에, 최악의 시간복잡도는 O(N^2)입니다.
하지만 pivot을 어떻게 잡냐에 따라서 시간복잡도가 달라지고, 평균적으로 O(NlogN)의 시간이 소요되며 다른 정렬들보다 월등히 빠릅니다.
개선된 pivot 선택방법으로는 다음과 같습니다.
- 데이터가 3개 이하면 피벗은 반드시 마지막 값이 됨
- 데이터가 4개 이상이면 맨 왼쪽, 오른쪽, 가운데 (나머지 버림) 값 중 중간 값을 선택함
- 피벗이 선택되면 먼저 구간의 맨 끝 원소와 꼭 교환해야함
Code
import java.io.*;
import java.util.*;
//Code Tree
public class Main {
static int N;
static int[] arr;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
arr = new int[N];
for (int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
quickSort(0, arr.length - 1);
for(int idx : arr) sb.append(idx).append(" ");
System.out.println(sb);
}
static int selectPivot(int low, int high) {
int diff = high - low;
if (diff <= 2) {
return high;
} else {
PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[1] - o2[1];
}
});
pq.offer(new int[]{low, arr[low]});
pq.offer(new int[]{high, arr[high]});
pq.offer(new int[]{low + (high - low) / 2, arr[low + (high - low) / 2]});
pq.poll();
return pq.poll()[0]; // 피벗의 인덱스를 반환
}
}
static int partition(int low, int high) {
int pivotIndex = selectPivot(low, high);
int pivot = arr[pivotIndex];
swap(pivotIndex, high); // 피벗을 끝으로 이동
int i = low - 1;
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swap(i, j);
}
}
swap(i + 1, high);
return i + 1;
}
static void quickSort(int low, int high) {
if (low < high) {
int pos = partition(low, high);
quickSort(low, pos - 1);
quickSort(pos + 1, high);
}
}
static void swap(int x, int y) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
}
힙 정렬
heap이라는 자료구조를 이용하면, N개의 원소들 중 최댓값을 찾는 것을 O(logN)만에 할 수 있게 됩니다. heap은 이진 트리 형태를 띄고 있습니다. 이진 트리의 경우 배열로 구현이 가능합니다.
배열로 구현하게 될 경우 특정 노드의 위치가 i라고 한다면, 자연스럽게 왼쪽 자식의 위치는 i * 2, 오른쪽 자식의 위치는 i * 2 + 1이 됩니다.
특정 노드 i의 자식 노드를 조회하기 위해서는 i * 2, i * 2 + 1을 하면 됩니다.
이렇게 이진트리를 띄는 구조 안에서, 모든 노드에 대해 부모 노드가 자신의 자식 노드가 갖는 값보다 같거나 큰 경우를 만족한다면 이를 max-heap 이라 합니다. Max Heap의 가장 중요한 특징 중 하나는, 루트 노드에는 전체 숫자 중 최댓값이 항상 들어 있다는 것입니다.
우선 배열로 구현한 이진트리를 max-heap구조로 만들기 위해 heapify 과정을 진행해야합니다.
heapify란 현재 노드를 기준으로 이 노드가 heap 특성에 맞을 때까지 계속 밑으로 내려주는 과정을 일컫습니다.
n / 2번째 원소부터 거꾸로 1번째 원소까지 순서대로 보면서 heapify라는 과정을 거치게 됩니다.
- 현재 노드 i와 왼쪽 자식, 오른쪽 자식을 비교하여 가장 큰 노드를 탐색합니다.
- 만약 가장 큰 노드가 현재 노드가 아니라면 현재 노드와 자리를 변경합니다. 교환 이후에는 변경된 가장 큰 노드 자리에서 heapify를 다시 진행합니다.
- 만약 가장 큰 노드가 현재 노드 i라면 종료합니다. (ex : leafnode)
heapify과정이 종료 후, max-heap구조가 완료되었다면 오름차순 정렬을 위해 1번 노드와 N번 노드의 위치를 변경해줍니다. 변경 후 max-heap 특성이 깨져버리기 때문에, heapify(1)을 진행하여 다시 맞추어야 합니다. 맞춘 후 다시 1번과 N번 자리를 변경하는 재귀를 통해 N이 1이 될 때 까지 계속 반복합니다.
heap은 이진트리 중에서도 왼쪽으로 가득 채워져있는 완전 이진 트리 모양으로 되어있기 때문에 트리의 높이가 logN이 됩니다. 따라서 heapify 과정은 한 번 일어날 때 최대 logN번 일어나게 됩니다.
따라서 heap sort의 경우 시간복잡도는 O(NlogN)이 됩니다.
Code
import java.io.*;
import java.util.*;
//Code Tree
public class Main {
static int N;
static int[] arr;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
N = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
arr = new int[N+1];
for (int i = 1; i<=N; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
heapSort(N);
for(int i=1; i<=N; i++) sb.append(arr[i]).append(" ");
System.out.println(sb);
}
static void heapify(int n, int i) {
int largest = i;
int l = i*2;
int r = i*2+1;
//case 1. 가장 큰 노드 탐색
if(l<=n && arr[l] > arr[largest]) {
largest = l;
}
if(r<=n && arr[r] > arr[largest]) {
largest = r;
}
//case 2. 가장 큰 노드가 현재 노드가 아닐 경우 재귀 진행
if(largest != i) {
swap(i, largest);
heapify(n, largest);
}
}
static void heapSort(int n) {
//1. Max-heap 만들기
for (int i = n / 2; i >= 1; i--) {
heapify(n, i);
}
//2. 정렬
for(int i=n; i>1; i--) {
swap(1, i);
heapify(i-1, 1);
}
}
static void swap(int x, int y) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
}
Stable Sort
회원 정보가 주어질 때, 고객들을 누적 포인트 순으로 정렬하되, 포인트가 같다면 먼저 가입한 사람이 앞에 나오도록 해야하는 상황에 같은 값을 넣어 정렬을 하였을 때, 먼저 들어간 값이 반드시 앞쪽에 있음이 보장된다면, 우리는 이런 정렬을 "Stable"하다고 합니다.
아쉽게도, 모든 정렬 알고리즘은 Stable하지 않습니다. 즉 저런 상황에 놓인 경우, 아무 정렬 알고리즘이나 사용할 수 없습니다.
Stable한 정렬 알고리즘의 경우 거품 정렬, 삽입 정렬, 병합 정렬, 기수 정렬이 있습니다.
In-Place Sort
In-Place Sort란 추가적인 메모리 없이 정렬이 가능한 알고리즘을 뜻합니다.
해당하는 알고리즘으로는 거품 정렬, 선택 정렬, 삽입 정렬, 퀵 정렬, 힙 정렬이 있습니다.
'CS > 알고리즘' 카테고리의 다른 글
| [PS] 백준1339 : 단어 수학(Java) (0) | 2024.10.07 |
|---|---|
| [PS] 백준13305 : 주유소(Java) (0) | 2024.10.05 |
| [코드트리 조별과제] 3주차 학습 (0) | 2024.07.30 |
| [PS] 백준1967 : 트리의 지름(Java) (0) | 2024.06.01 |
| [PS] 백준2003 : 수들의 합 2(JAVA) - 투 포인터 활용편 (2) | 2024.03.23 |

개발 기술 블로그, Dev
포스팅이 좋았다면 "좋아요❤️" 또는 "구독👍🏻" 해주세요!
![[PS] 백준1339 : 단어 수학(Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FcoH5X4%2FbtsJWAqbo90%2FAAAAAAAAAAAAAAAAAAAAAKsuj4iuxBYVyt0PfPZvkuFP-7Npxmmmpr7NShKWj5Oc%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3D93i%252F%252FPDhCsKPnewofITXKJ2zDQk%253D)
![[PS] 백준13305 : 주유소(Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FdFyBda%2FbtsJU2UY4cY%2FAAAAAAAAAAAAAAAAAAAAAFsXXdUTcPFlpZcKtLWF5pEMmh8lmN9VOCyR-kFSaU_w%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3Dopp5xeAjTvEw3caufbokEe7oDu8%253D)
![[코드트리 조별과제] 3주차 학습](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FkBs3x%2FbtsIQyGMAnt%2FAAAAAAAAAAAAAAAAAAAAAAx5coQEhwxICC2nqC1E2yKCrP82Vm5wH0TJgqdDAKDr%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DOLyJ%252FHUkqGdYy%252Fju7UBhKmwlT0M%253D)
![[PS] 백준1967 : 트리의 지름(Java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fb580Z1%2FbtsHLUXeEWF%2FAAAAAAAAAAAAAAAAAAAAAGm-5JLUcanenfB6erXxnDc-7eGR2RkmSlVNA8tGAbDq%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1764514799%26allow_ip%3D%26allow_referer%3D%26signature%3DbTslvxF0JppGwO4GttXS9%252BsrCH0%253D)